The indicators in the column “Limit bullet flight range” are calculated at a bullet departure angle relative to the horizon of 31°, since it is believed that the greatest bullet flight range is obtained at angles of 30-32°. In practice, this angle when firing a bullet is much smaller: usually a bullet is fired at large animals at a distance of no further than 60 m, and the angle between the horizon and the direction of the aiming line is zero, which indicates the coincidence of these lines.
The exception is shooting at an animal in mountainous conditions from bottom to top. In this case, the angle of departure of the bullet relative to the horizon can be any and correspond to the maximum flight range of the bullet, which must be taken into account when hunting in the mountains or very rough terrain. This is especially important for a hunt leader or huntsman to know during group hunts, when they have to place hunters in numbers so that they do not hit each other when shooting.
A little story
In 1537, Niccolò Tartaglia fired several test shots to determine the maximum angle and range of the bullet.
Tartaglia concluded that the angle was 45 degrees. The mathematician noted that the trajectory of the shot is constantly bending. In 1636, Galileo Galilei published his results in Dialogues on the Two New Sciences. He discovered that a falling body has constant acceleration. This allowed Galileo to show that the bullet's trajectory was curved.
Around 1665, Isaac Newton discovered the law of air resistance. Newton used air and liquids in his experiments. He showed that shot resistance increases in proportion to air (or liquid) density, cross-sectional area and bullet weight. Newton's experiments were carried out only at low speeds - up to about 260 m/s (853 ft/s).
In 1718 John Keel challenged Continental Mathematics. He wanted to find the curve that a projectile could describe in the air. This problem assumes that air resistance increases exponentially with the speed of the projectile. Keel could not find a solution to this difficult problem. But Johann Bernoulli set out to solve this difficult problem and soon after found the equation. He realized that air resistance varies as "any force" of speed. This proof later became known as the Bernoulli equation. It is this that is the forerunner of the “standard projectile” concept.
Armament of the T-80 tank
The T-80 tank became famous for being the world's first combat vehicle with a gas turbine engine. It allowed us to reduce the time required to prepare the machine for further operation. Due to the fact that there was no longer any need to warm up the engine, the car could:
- Start driving immediately in above-zero temperatures.
- Proceed with redeployment 2-3 minutes after starting the power plant at an ambient temperature of -18 degrees Celsius.
- Start driving after 20-30 minutes in more severe climate conditions.
At the moment it is an outdated model, but is still in service in some countries. Was developed in 1976. The main weapon is a 125 mm 2A46-1 type gun.
The firing range of the T-80 tank from the main gun is about 3,700 meters. At the beginning of its production it was not equipped with guided missiles. Subsequent modifications of the equipment acquired ATGM installations, and the missile range was about 5 kilometers.
Historical inventions
In 1742, Benjamin Robins created the ballistic pendulum. It was a simple mechanical device that could measure the speed of a projectile. Robins reported bullet velocities ranging from 1,400 ft/s (427 m/s) to 1,700 ft/s (518 m/s). In his book New Principles of Shooting, published the same year, he used Euler's method of numerical integration and found that air resistance "varies as the square of the velocity of the projectile."
In 1753, Leonhard Euler showed how theoretical trajectories could be calculated using Bernoulli's equation. But this theory can only be used for resistance varying as the square of the speed.
In 1844, the electroballistic chronograph was invented. In 1867, this device showed the time of flight of a bullet with an accuracy of one tenth of a second.
TABLE DATA ON EXTERNAL BALLISTICS OF AN AMERICAN CARTRIDGE EQUIPPED WITH A BRENNEKE BULLET
| Weapon caliber | Mass of bullet with wad g, | Length trunk mm | Bullet flight speed, m/s | Bullet energy, kgf/m | ||||||||
| distance, m | ||||||||||||
| 0 | 23 | 46 | 69 | 91 | 0 | 23 | 46 | 69 | 91 | |||
| 12th | 31,8 | 762 | 485 | 421 | 369 | 330 | 298 | 380 | 290 | 220 | 178 | 146 |
| 16th | 27.8 | 710 | 460 | 397 | 344 | 304 | 275 | 300 | 224 | 169 | 131 | 107 |
| 20th | 23,7 | 710 | 462 | 396 | 342 | 301 | 271 | 259 | 190 | 142 | 110 | 89 |
Weapon caliber | Bullet flight path cm | |||||||
| distance, m | ||||||||
| I | II | |||||||
| 23 | 46 | 69 | 91 | 23 | 46 | 69 | 91 | |
| 12th | + 0,61 | ——— | — 4 | — 12,6 | -0,89 | ——- | -2,6 | -9,8 |
| + 1.9 | + 2,7 | ——— | — 8 | -0,2 | + 1,8 | ——- | -6,4 | |
| + 3,71 | + 6,3 | + 4,3 | ——— | + 1,3 | + 4,9 | + 4,8 | —— | |
| 16th | + 0,89 | ——— | — 4,8 | — 15 | -0,2 | ——— | -3,2 | -12,2 |
| + 2,5 | + 3.2 | ——— | — 8,7 | + 0,6 | + 2,2 | ——— | -7,7 | |
| 20th | + 5,72 | + 9,6 | + 9,5 | ——— | + 3,5 | + 7,8 | + 8,3 | ——- |
Note.
I
- open sight, aiming line 2 cm above the center of the barrel; II - optical sight, the aiming line is 5 cm above the center of the barrel, the (+) sign indicates that the bullet will fly above the aiming line, the (-) sign indicates that the bullet will fly below the aiming line.
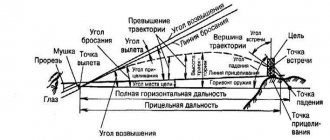
Rice. 45.
Trajectory of the central part of the shot sheaf (schematic representation):
1 — aiming line; 2 — flight path of the central part of the shot sheaf; 3 — direction of the bore axis; Ө0 is the angle between the axis of the barrel bore and the aiming line, depending on the design of the sighting devices on the gun; O - the point of intersection of the bore axis with the aiming line; AB, GI and EL are the magnitudes of the trajectory decrease at various distances. BV, ID and LC - the magnitude of the excess of the trajectory above the aiming line.
Test run
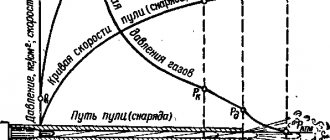
Many countries and their militaries have conducted test firings using large ammunition to determine the drag characteristics of each individual projectile since the mid-18th century.
These individual test experiments were recorded in extensive ballistic tables. Serious tests were carried out in England (the tester was Francis Bashforth, the experiment itself was carried out on the Woolwich Marshes in 1864). The projectile reached a speed of up to 2800 m/s. Friedrich Krupp continued testing in 1930 (Germany).
The shells themselves were solid, slightly convex, with a cone-shaped tip. They ranged in size from 75 mm (0.3 in) with a weight of 3 kg (6.6 lb) to 254 mm (10 in) with a weight of 187 kg (412.3 lb).
Methods and standard projectile
Many military personnel before the 1860s used the calculus method to correctly determine the trajectory of a projectile. This method, which was suitable for calculating only one trajectory, was performed manually. To make calculations much easier and faster, research began on creating a theoretical resistance model. Research has led to a significant simplification of experimental processing. This was the "standard projectile" concept. Ballistic tables were compiled for a contrived projectile with a given weight and shape, specific dimensions and a specific caliber. This simplified the calculation of the ballistic coefficient of a standard projectile, which could move through the atmosphere according to a mathematical formula.
Ballistic coefficient table
The above-mentioned ballistic tables usually include the following functions: air density, time of flight of the projectile in the range, range, degree of deviation of the projectile from a given trajectory, weight and diameter.
These indicators facilitate the calculation of ballistic formulas, which are needed in order to calculate the initial velocity of the projectile in the range and flight path. The 1870 Bashforth barrels fired a projectile at 2800 m/s. For calculations, Mayevsky used the tables of Bashfort and Krupp, which included up to 6 zones with limited access. The scientist conceived a seventh restricted zone and stretched the Bashfort trunks to 1,100 m/s (3,609 ft/s). Mayevsky converted the data from imperial units of measurement to metric units (currently SI units).
In 1884, James Ingalls presented his barrels in the US Army Ordnance Circular using Majewski's tables. Ingalls expanded the ballistic barrels to 5000 m/s, which were within the eighth restricted zone, but still with the same n value (1.55) as Mayevsky's 7th restricted zone. The fully improved ballistic tables were published in 1909. In 1971, Sierra Bullet calculated its ballistic tables for 9 limited zones, but only within 4,400 feet per second (1,341 m/s). This zone has lethal force. Imagine a projectile weighing 2 kg flying at a speed of 1341 m/s.
Flight speed and trajectory
There is another factor that affects the flight range - the initial speed of the projectile. Accordingly, the lower the initial acceleration, the closer the enemy tank should be located. The firing range also depends on the throwing angles, which, in turn, are again determined by the initial speed. The more meters per second the cannonball travels during flight, the smaller the angle must be set to hit the target.
All of the above factors - derivation, throwing angle, initial flight force - set the trajectory of the projectile. The main task facing engineers at this stage of development of tank technology is to give the projectile a more direct glide path - a vertical flight line. Now it is a parabola.
Mayevsky method
We have already mentioned this name a little above, but let’s look at what kind of method this man came up with. In 1872, Majewski published the report Trité Balistique Extérieure. Using his ballistic tables along with Bashforth's tables from the 1870 report, Majewski created an analytical mathematical formula that calculated the air resistance for a projectile in terms of log A and the value of n. Although the scientist used a different approach in mathematics than Bashforth, the resulting calculations of air resistance were the same. Mayevsky proposed the concept of a limited zone. While exploring, he discovered the sixth zone.
Around 1886, the general published the results of a discussion of the experiments of M. Krupp (1880). Although the projectiles used varied widely in caliber, they had essentially the same proportions as a standard projectile, measuring 3 meters in length and 2 meters in radius.
Siacci method
In 1880, Colonel Francesco Siacci published his work Balistica.
Siacci theorized that air resistance and density become greater as the projectile's speed increases. The Siacci method was intended for flat-fire trajectories with deflection angles less than 20 degrees. He discovered that such a small angle did not allow the air density to have a constant value. Using the tables of Bashforth and Mayevsky, Siacci created a 4-zone model. Francesco used a standard projectile created by General Mayevsky.
Bullet ballistic coefficient
A bullet's ballistic coefficient (BC) is basically a measure of how streamlined a bullet is, that is, how well it cuts through the air. Mathematically, it is the ratio of a bullet's specific density to its aspect ratio. Ballistic coefficient is essentially a measure of air resistance. The higher the number, the less resistance, and the more effectively the bullet penetrates the air.
Another meaning is BC. The indicator determines the trajectory and drift of the wind when other factors are equal. BC changes with the shape of the bullet and the speed at which it travels. "Spitzer", which means "directional", is a more effective shape than "round nose" or "flat point". At the other end of the bullet, the boat tail (or tapered heel) reduces air resistance compared to a flat base. Both increase the bullet's BC.
Bullet Scattering
In addition, there is still a certain dispersion of bullets when shooting at a distance of 69 m. If the dispersion diameter is 30 cm when shooting at a distance, then the bullet can hit either 15 cm above the calculated point of impact (it is 4.3 cm higher than the aiming point), or lower by the same amount (half the dispersion diameter), i.e. the bullet can hit either above the aiming point by 19.3 cm (4.3 cm + 15 cm), or below it by 10.7 cm (15-4.3 cm) .
If the vital organs of the animal being shot are located in the calculated area from the aiming point (10.7 cm below and 19.3 cm above), then the game will be hit. The area where the animal's vital organs are located is called the slaughter zone. For each animal it has its own value, and the greater the height, the further the direct shot will be (all other things being equal). The greater the range of a direct shot, the less the inaccuracy in determining the distance from the animal being shot will affect the accuracy of the hit.
Bullet range
Of course, each bullet is different and has its own speed and range.
Firing the rifle at an angle of about 30 degrees will give the longest flight distance. This is a really good angle as an approximation to optimal performance. Many people assume that 45 degrees is the best angle, but this is not true. The bullet is affected by the laws of physics and all natural forces that can interfere with an accurate shot. After the bullet leaves the barrel, gravity and air resistance begin to work against the starting energy of the muzzle wave, and lethal force develops. There are other factors, but these two have the greatest impact. As soon as the bullet leaves the barrel, it begins to lose horizontal energy due to air resistance. Some people will tell you that the bullet rises as it leaves the barrel, but this is only really true if the barrel was placed at an angle when fired, which is often the case. If you shoot horizontally towards the ground and throw the bullet upward at the same time, both projectiles will hit the ground at almost the same time (minus the minor differential caused by the curvature of the earth and the slight drop in vertical acceleration).
If you aim a gun at an angle of about 30 degrees, the bullet will travel much further than many people realize, and even a low-energy weapon like a pistol will send the bullet over a mile. A projectile from a high-powered rifle can travel approximately 3 miles in 6-7 seconds, so under no circumstances should you shoot into the air.
Information from external ballistics
External ballistics -
is a science that studies the movement of a bullet (grenade) after the action of powder gases on it ceases.
Having flown out of the bore under the influence of powder gases, the bullet (grenade) moves by inertia. A grenade with a jet engine moves by inertia after the gases flow out of the jet engine.
Trajectory and its elements
Trajectory
called the curved line described by the center of gravity of the bullet in flight.
When flying in the air, a bullet is subject to two forces: gravity and air resistance.
The force of gravity causes the bullet to gradually lower, and the force of air resistance continuously slows down the movement of the bullet and tends to knock it over.
As a result of the action of these forces, the speed of the bullet gradually decreases, and its trajectory is shaped like an unevenly curved curved line.
| Trajectory parameters | Parameter characteristics | Note |
| 1. Departure point | Center of the muzzle of the barrel | The departure point is the beginning of the trajectory |
| 2. Weapon horizon | Horizontal plane passing through the departure point | The weapon horizon looks like a horizontal line. The trajectory crosses the horizon of the weapon twice: at the point of departure and at the point of impact |
| 3. Elevation line | A straight line that is a continuation of the axis of the barrel of the aimed weapon | |
| 4. Elevation angle | The angle between the elevation line and the horizon of the weapon | If this angle is negative, then it is called the declination (decrease) angle |
| 5. Throwing line | Straight, a line that is a continuation of the axis of the bore at the moment the bullet leaves | |
| 6. Throwing angle | The angle between the throwing line and the horizon of the weapon | |
| 7. Departure angle | The angle between the elevation line and the throwing line | |
| 8. Drop point | The point of intersection of the trajectory with the horizon of the weapon | |
| 9. Angle of incidence | The angle between the tangent to the trajectory at the point of impact and the horizon of the weapon | |
| 10. Full horizontal range | Distance from departure point to impact point | |
| 11. Top of the trajectory | Highest point of the trajectory | |
| 12. Trajectory height | Shortest distance from the top of the trajectory to the horizon of the weapon | |
| 13. Exceeding the trajectory above the aiming line | The shortest distance from any point on the trajectory to the aiming line | |
| 14. Target elevation angle | The angle between the line of sight and the horizon of the weapon | The target's elevation angle is considered positive (+) when the target is above the weapon's horizon, and negative (-) when the target is below the weapon's horizon. |
| 16. Meeting point | The point of intersection of the trajectory with the target surface (ground, obstacles) | |
| 17. Aiming point (aiming) | The point on or off the target at which the weapon is aimed | |
| 18. Meeting angle | The angle between the tangent to the trajectory and the tangent to the surface of the target (ground, obstacle) at the meeting point | The meeting angle is taken to be the smaller of the adjacent angles, measured from 0 to 90° |
| 19. Line of sight | A straight line running from the shooter's eye through the middle of the sight slot (level with its edges) and the top of the front sight to the aiming point | |
| 20. Sighting range | Distance from the departure point to the intersection of the trajectory with the aiming line | |
| 21. Aiming angle | The angle between the elevation line and the aiming line | |
| Vertical aiming | Giving the bore axis the required position in the vertical plane | |
| Ascending branch | Part of the trajectory from the departure point to the top | |
| Horizontal aiming | Giving the bore axis the required position in the horizontal plane | |
| Target line | Straight line connecting the departure point to the target | When firing direct fire, the target line practically coincides with the aiming line |
| Slant range | Distance from departure point to target along target line | When firing direct fire, the slant range practically coincides with the target range. |
| Descending branch | Part of the trajectory from the top to the point of fall | |
| Final speed | Bullet speed at impact point | |
| Firing plane | Vertical plane passing through the elevation line | |
| Total flight time | Time of movement of a bullet from the point of departure to the point of impact | |
| Aiming (aiming) | Giving the axis of the weapon barrel the necessary position in space for shooting | In order for the bullet to reach the target and hit it or the desired point on it |
| Sight line | A straight line connecting the middle of the sight slot to the top of the front sight |
Direct shot
Straight shot
called a shot in which the flight path of the bullet does not rise above the aiming line above the target along its entire length. The range of a direct shot depends on the height of the target and the flatness of the trajectory. The higher the target and the flatter the trajectory, the greater the direct shot range and, therefore, the distance at which the target can be hit with one sight setting.
Practical meaning of a straight shot
lies in the fact that in tense moments of battle, shooting can be carried out without rearranging the sight, while the aiming point in height will be selected along the lower edge of the target.
Each shooter must know the range of a direct shot at various targets from his weapon and skillfully determine the range of a direct shot when shooting.
The direct shot range can be determined from tables by comparing the target height with the values of the greatest elevation above the aiming line or with the trajectory height.
Straight shot and rounded straight shot ranges
from small arms of 5.45 mm caliber
When firing, you need to know that the distance on the ground, over which the downward branch of the trajectory does not exceed the height of the target, is called the target space
(depth of the affected space Ppr.).
Depth (Ppr.)
depends:
on the height of the target (the higher the target, the higher it will be);
on the flatness of the trajectory (the flatter the trajectory, the greater it will be);
on the angle of inclination of the terrain (on the front slope it decreases, on the reverse slope it increases).
The depth of the affected space (Dpr.) can be determined from tables of trajectory elevations above the aiming line by comparing the excess of the descending branch of the trajectory at the corresponding firing range with the target height, and if the target height is less than 1/3 of the trajectory height, using the thousandth formula:
where Ppr
— depth of the affected space in m;
Vts
— target height in m;
β
is the angle of incidence in thousandths.
The space behind cover that is not penetrated by a bullet, from its crest to the meeting point is called covered space
. The greater the height of the shelter and the flatter the trajectory, the greater the covered space.
The part of the covered space in which the target cannot be hit with a given trajectory is called dead (unhittable) space.
The greater the height of the cover, the lower the height of the target and the flatter the trajectory, the greater the dead space. The other part of the covered space (Sp), in which the target can be hit, is the target space.
The depth of dead space (Mpr.) is equal to the difference between the covered and affected space:
Mpr = Pp - Ppr
Knowledge of the value of Pp. and Mpr. allows you to correctly use shelters to protect against enemy fire, as well as take measures to reduce dead spaces by correctly choosing firing positions and firing at targets from weapons with a more forward trajectory.
Normal (tabular) shooting conditions
The tabulated trajectory data corresponds to normal shooting conditions.
The following are accepted as normal (tabular) conditions:
Weather conditions:
· atmospheric (barometric) pressure at the horizon of the weapon is 750 mm Hg. Art.;
· air temperature on the horizon of the weapon +15° C;
· relative air humidity 50% (relative humidity is the ratio of the amount of water vapor contained in the air to the largest amount of water vapor that can be contained in the air at a given temperature);
· there is no wind (the atmosphere is motionless).
Ballistic conditions:
· bullet weight, initial speed and departure angle are equal to the values indicated in the shooting tables;
· charge temperature +15°С;
· the shape of the bullet corresponds to the established drawing;
· the height of the front sight is set based on the data of bringing the weapon to normal combat;
· the heights (divisions) of the sight correspond to the table aiming angles.
Topographic conditions:
· the target is on the horizon of the weapon;
· There is no lateral tilt of the weapon.
If shooting conditions deviate from normal, it may be necessary to determine and take into account corrections for the firing range and direction.
The influence of external factors on the flight of a bullet
As atmospheric pressure increases, air density increases, and as a result, the force of air resistance increases and the bullet's flight range decreases. On the contrary, with a decrease in atmospheric pressure, the density and force of air resistance decrease, and the bullet’s flight range increases.
As the temperature rises, the air density decreases, and as a result, the force of air resistance decreases and the bullet's flight range increases. On the contrary, as the temperature decreases, the density and force of air resistance increase, and the bullet’s flight range decreases.
With a tailwind, the speed of the bullet relative to the air decreases. As the speed of the bullet relative to the air decreases, the force of air resistance decreases. Therefore, with a tailwind, the bullet will fly further than with no wind.
In a headwind, the speed of the bullet relative to the air will be greater than in a calm environment, therefore, the force of air resistance will increase and the bullet's flight range will decrease.
Longitudinal (tailwind, headwind) wind has an insignificant effect on the flight of a bullet, and in the practice of shooting from small arms, corrections for such wind are not introduced.
The side wind puts pressure on the side surface of the bullet and deflects it away from the firing plane depending on its direction: the wind from the right deflects the bullet to the left, the wind from the left to the right.
Wind speed is determined with sufficient accuracy by simple signs: in a weak wind (2-3 m/sec), the handkerchief and flag sway and flutter slightly; in moderate winds (4-6 m/sec), the flag is kept unfurled and the scarf flutters; in a strong wind (8-12 m/sec), the flag flutters noisily, the scarf is torn from the hands, etc.
Changes in air humidity have a negligible effect on air density and, therefore, on the range of a bullet, so it is not taken into account when shooting.
Penetrating (killing) effect of a bullet
For firing from a machine gun, cartridges with ordinary (steel core) and tracer bullets are used. The lethality of a bullet and its penetrating effect mainly depends on the range to the target and the speed that the bullet will have at the moment it meets the target.
| Item no. | Name of the obstacle (protective equipment) | Firing range, m. | % through penetration or bullet penetration depth |
| 1 | Steel sheets (at a meeting angle of 90°) thickness: | ||
| 2 mm. | 950 | 50% | |
| 3 mm. | 670 | 50% | |
| 5 mm. | 350 | 50% | |
| 2 | Steel helmet (helmet) | 800 | 80-90% |
| 3 | Body armor | 550 | 75-100% |
| 4 | Parapet made of dense compacted snow | 400 | 50-60 cm. |
| 5 | Earthen barrier made of compacted loamy soil | 400 | 20-25 cm. |
| 6 | Wall made of dry pine beams 20 cm thick. | 650 | 50% |
| 7 | Brickwork | 100 | 10-12 cm. |
Thousandth formula and its application
In shooting practice, the unit of measurement of angles (measure of angles) is the central angle, the arc length of which is equal to 1/6000 of the circumference. This angular unit is called the division of the protractor. As is known from geometry, the circumference of a circle is 2πR, or 6.28 R (R is the radius of the circle).
If a circle is divided into 6000 equal parts, then each part will be equal to:
The length of the arc corresponding to this angle is equal to 1/955 (rounded to 1/1000) the length of the radius of this circle.
Therefore, the division of a protractor is usually called thousandths. The relative error that results from this rounding is equal to 4.5%, or rounded to 5%, i.e., the thousandth is 5% less than the protractor division. In practice, this error is neglected.
The protractor division (thousandths) allows you to easily move from angular units to linear ones and back, since the arc length corresponding to the protractor division at all distances is equal to one thousandth the length of the radius equal to the firing range.
An angle of one thousandth corresponds to an arc that is equal at a distance of 1000 m - 1 m (1000 m: 1000), at a distance of 500 m - 0.5 m (500: 1000), at a distance of 250 m - 0.25 m (250: 1000), etc. d.
An angle of several thousandths corresponds to arc length B
, equal to one thousandth of the range
(D/1000)
, multiplied by the angle containing
Y
thousandths, i.e.
The resulting formulas are called thousandth formulas and are widely used in shooting practice. In these formulas D
— the distance to the object in meters.
Y
is the angle at which the object is visible in thousandths.
B
is the height (width) of the object in meters, i.e. the length of the chord, not the arc. At small angles (up to 15°), the difference between the length of the arc and the chord does not exceed one thousandth, therefore in practical work they are considered equal.
Measuring angles in goniometer divisions (thousandths) can be done: with a compass goniometric circle, binocular and periscope reticle, an artillery circle (on a map), the entire sight, the lateral correction mechanism of a sniper scope and improvised objects. The accuracy of angular measurement using a particular device depends on the accuracy of the scale on it.
When using improvised objects to measure angles, it is necessary to determine their angular value in advance. To do this, you need to extend your hand with a handy object at eye level and notice any points on the ground at the edges of the object, then using a goniometric device (binoculars, compass, etc.) accurately measure the angular value between these points.
The angular size of a handy object can also be determined using a millimeter ruler. To do this, the width (thickness) of the object in millimeters must be multiplied by 2 thousandths, since one millimeter of a ruler when it is 50 cm away from the eye corresponds, according to the thousandth formula, to an angular value of 2 thousandths.
Angles expressed in thousandths are written through a dash and read separately: first hundreds, and then tens and units; if there are no hundreds or tens, zero is written and read. For example: 1705 thousandths are written 17-05, read - seventeen zero five; 130 thousandths are written 1-30, read - one thirty; 100 thousandths are written as 1-00, read as one zero; one thousandth is written 0-01, read - zero zero one.
Test
External ballistics is a science:
about the movement of a bullet (projectile) in mountainous areas. about the movement of a bullet (projectile) in the air. about the movement of a bullet (projectile) in the bore of a weapon and the processes accompanying the movements. about the movement of a bullet (projectile) in a confined space.
The trajectory is called:
called the straight line described by the center of gravity of the bullet. called the line described by the bullet. called the curved stripe described by a bullet in flight. called the curved line described by the center of gravity of the bullet in flight
A direct shot is called:
a shot in which the trajectory of the projectile throughout its entire length to the target rises above the target and does not fall below its base. a shot in which the trajectory of the projectile throughout its entire length to the target does not rise above the target and falls below its base. a shot in which the trajectory of the projectile throughout its entire length to the target does not rise above the target and does not fall below its base. the beginning of combustion of the powder charge until the bullet casing is completely embedded in the rifling of the barrel.
Direct shot range is:
such a firing range at which the height of the trajectory is equal to the height of the target; it can also be defined as the greatest distance to the target at which it is still possible to receive a direct shot. such a firing range at which the height of the trajectory is not equal to the height of the target, it can also be defined as the greatest range to the target at which it is still possible to receive a direct shot. such a firing range at which the height of the trajectory is equal to the height of the target, it can also be defined as the greatest range to the target, at which it is no longer possible to receive a direct shot. a complex thermodynamic process of very rapid, almost instantaneous conversion of the chemical energy of gunpowder into thermal, and then into the kinetic energy of powder gases that propel the bullet.
Ballistic coefficient of air bullets
Air bullets were not designed to hit a target, but to stop a target or cause minor physical harm. In this regard, most airgun bullets are made from lead, since this material is very soft, lightweight and gives the projectile a low initial velocity. The most common types of bullets (calibers) are 4.5 mm and 5.5. Of course, larger caliber ones were also created - 12.7 mm. When firing from such a pneumatic gun and such a bullet, you need to think about the safety of strangers. For example, ball-shaped bullets are made for entertaining games. In most cases, this type of projectile is coated with copper or zinc to avoid corrosion.
Armament of the T-90 tank
The main weapon of the T-90 tank is a 125-mm smoothbore cannon, which is paired with a machine gun mount and mounted on trunnions, providing greater flexibility when aiming at a target. The stabilization system is represented by the “Jasmine” design. The new gun has great shooting accuracy and fast reloading - about 6.5 seconds due to the automatic loader.
One of the exceptional features of the gun is the ability to fire guided missiles. The firing range of the T-90 tank with ATGM guns is 5 km. This is ensured by modern designs of both guidance systems and the missile itself.
The missile control complex is represented by a laser guidance channel with a ballistic computer, an automated control unit and the shots themselves, which are fired by guided missiles for a tank gun. The presented engineering solutions make it possible to hit both stationary targets and those moving at speeds of more than 70 km/h with an accuracy of more than 60%.