1.9.4.1.4. Flatness of bullet flight path or ease of aiming
1.9.4.1.4. Flatness of bullet flight path or ease of aiming
When choosing a bullet, in addition to the possibility of reliably hitting a target, it is also necessary to take into account the probability of hitting a specific target at various distances. In table
18 shows the excess of the trajectories above the aiming line. If the trajectory height does not exceed the target height, then the bullet will hit the target at all closer distances. It is clear that in hunting practice it is very difficult to accurately determine the distance to the animal, so the excess of the trajectory above the aiming line is of great importance. When shooting at 100 m from a rifle chambered for 5.6×16 (rimfire) with the appropriate installation of the sight, the maximum elevation of the trajectory above the aiming line will reach 13–14 cm.
If an error was made in determining the distance by 25% in one direction or another, then with an actual distance to the target of 75 m, the bullet at the target will go 12 cm above the aiming point, and at an actual distance of 125 m - below the aiming point by 18 cm. When firing the specified cartridge at a distance of 100 m, the dispersion reaches a diameter of 7.2 cm. If, as indicated above, the distance turned out to be 75 m rather than 100 m, then the bullets can travel within the range of 9 to 15 cm above the aiming point (12 cm ± 0.5 dispersion diameter), and if 125 m, then in the range from 12.5 to 23.5 cm below it.
Since shooting from this rifle is carried out at small animals and birds, the probability of a fatal hit at such distances will be small, and the probability of wounding an animal due to hitting a non-killing place will be high. Therefore, rifles chambered for 5.6×16 provide reliable hits on targets only at distances up to 50 m.
The 9?53 hunting cartridge is intended for shooting at large animals.
The size of the target is determined by the size of those parts of the animal’s body that will be lethal when hit. When shooting at an elk and aiming at the shoulder blade, a kill will be quite reliable if the bullet does not leave the circle with a diameter of 20 cm (does not deviate up and down from the aiming point by more than 10 cm). In this case, vital centers will be affected. In terms of combat accuracy, the 9?53 cartridge will provide this condition at a distance of 300 m and even slightly more. At the same distance, the excess of the trajectory is already 45 cm, that is, an error in determining the distance can lead the bullet out of the circle we have accepted. At a distance of 400 m, the excess of the trajectory above the aiming line will already be greater than 0.7 m, and the dispersion diameter will be close to 25 cm. In other words, inaccuracies in determining the distance and dispersion can easily lead the bullet not only beyond the slaughter area, but also beyond the boundaries of the goals. The likelihood of non-fatal injuries and near misses becomes high.
The 5.6×39 hunting cartridge gives the best performance in this regard, however, it is intended for shooting at medium-sized, not large, animals. Considering those placed in the table. 18
data for this cartridge, it is not difficult to determine, based on them and the size of the targets, that, for example, when shooting at a fox, a reliable hit beyond a 200-meter distance is hardly possible. When shooting at a large roe deer, this distance can increase to 300 m, but no more. From the foregoing, it becomes clear that, if possible, you should choose a cartridge in which the excess of the bullet’s flight path above the aiming line is minimal.
The shape of the trajectory and its practical significance
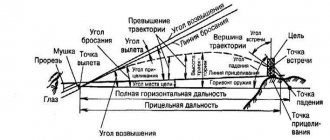
42. The shape of the trajectory depends on the magnitude of the elevation angle. As the elevation angle increases, the trajectory height and the full horizontal flight range of the bullet (grenade) increase, but this occurs to a certain limit. Beyond this limit, the trajectory height continues to increase, and the total horizontal range begins to decrease (Fig. 15).
The elevation angle at which the full horizontal flight range of a bullet (grenade) becomes greatest is called the angle of greatest range
. The maximum range angle for bullets of various types of weapons is about 35°.
Trajectories obtained at elevation angles less than the angle of greatest range are called flat.
.
Trajectories obtained at elevation angles greater than the angle of greatest range are called hinged
.
Rice. 15. Angle of greatest range, flat mounted and conjugate trajectories
When firing from the same weapon (at the same initial speeds), you can get two trajectories with the same horizontal range: flat and mounted. Trajectories that have the same horizontal range at different elevation angles are called conjugate
.
43. When firing from small arms and grenade launchers, only flat trajectories are used. The smoother the trajectory, the greater the area over which the target can be hit with one sight setting (the less impact errors in determining the sight setting have on the shooting results); This is the practical significance of the flat trajectory.
The flatness of the trajectory is characterized by its greatest excess above the aiming line. At a given range, the trajectory is flatter the less it rises above the aiming line. In addition, the flatness of the trajectory can be judged by the magnitude of the angle of incidence: the smaller the angle of incidence, the more flat the trajectory.
Example. Compare the flatness of the trajectory when firing from a Goryunov heavy machine gun and a Kalashnikov light machine gun with sight 5 at a distance of 500 m.
Solution. From the table of the excess of average trajectories over the aiming line and the main table, we find that when firing from a heavy machine gun at 500 m with sight 5, the greatest excess of the trajectory over the aiming line is 66 cm, the angle of incidence is 6.1 thousandths; when firing from a light machine gun - 121 cm and 12 thousandths, respectively. Consequently, the trajectory of a bullet when firing from a heavy machine gun is more flat than the trajectory of a bullet when firing from a light machine gun.
The flatness of the trajectory affects the range of the direct shot, the target, covered and dead space.
44. A shot in which the trajectory does not rise above the aiming line above the target along its entire length is called a direct shot
(Fig. 16).
Rice. 16. Straight shot
Within the range of a direct shot, during tense moments of battle, shooting can be carried out without rearranging the sight, while the vertical aiming point is usually selected at the lower edge of the target.
The range of a direct shot depends on the height of the target and the flatness of the trajectory. The higher the target and the flatter the trajectory, the greater the range of a direct shot and the greater the area over which the target can be hit with one sight setting.
The direct shot range can be determined from tables by comparing the target height with the values of the greatest elevation of the trajectory above the aiming line or with the trajectory height.
Example. Determine the direct shot range when firing from a Goryunov heavy machine gun at an enemy machine gun (target height 0.55 m).
Solution. Using the table of the excess of average trajectories above the aiming line by comparing the target height with the greatest excess of trajectories, we find: when shooting at 500 m with scope 5, the greatest elevation of the trajectory (0.66 m) is greater than the target height, and at 400 m with scope 4 it is (0. 36 m) less than the target height. Consequently, the direct shot range will be more than 400 m and less than 500 m.
To determine how much the direct shot range is greater than 400 m, let’s make a proportion: 100 m (500-400) increases the excess by 0.30 m (0.66 - 0.36); the target is 0.19 m (0.55–0.36) above the greatest elevation at 400 m. Hence, an elevation of the target equal to 0.19 m corresponds to an increase in the direct shot range by
The direct shot range will be 463 m (400+63), and the corresponding sight setting will be 4.5.
When solving the examples set out in this Manual, data taken from the tables of the relevant manuals on small arms in recent years of publication were used. They correspond to the data of the Tables of shooting at ground targets from small arms of 7.62 mm caliber No. 61, ed. 1962
45. When shooting at targets located at a distance greater than the direct shot range, the trajectory near its top rises above the target, and the target in some area will not be hit with the same sight setting.
However, there will be a space (distance) near the target at which the trajectory does not rise above the target and the target will be hit by it.
The distance on the ground over which the downward branch of the trajectory does not exceed the height of the target is called the affected space (the depth of the affected space)
. The depth of the affected space (Fig. 17) depends on the height of the target (it will be greater, the higher the target), on the flatness of the trajectory (it will be greater, the flatter the trajectory) and on the angle of inclination of the terrain (on the forward slope it decreases, on the reverse slope - increases).
The depth of the affected space (Dpr) can be determined from the tables of the excess of trajectories above the line of sight
by comparing the excess of the descending branch of the trajectory to the corresponding firing range with the target height, and if the target height is less than 1/3 of the trajectory height, using the thousandth formula:
where Ppr
— depth of the affected space in meters;
Vts
— target height in meters;
0c
is the angle of incidence in thousandths.
Rice. 17. Dependence of the depth of the affected space on the target height and partial trajectory (angle of incidence)
Example. Determine the depth of the affected area when firing from a Goryunov heavy machine gun at enemy infantry (target height B = 1.5 m) at a distance of 1000 m.
Solution. Using the table of excesses of average trajectories over the aiming line, we find: at 1000 m the excess of the trajectory is 0, and at 900 m it is 2.5 m (greater than the target height). Consequently, the depth of the affected space is less than 100 m. To determine the depth of the affected space, we create a proportion: 100 m corresponds to an excess of the trajectory of 2.5 m; X m corresponds to a trajectory exceeding 1.5 m:
Since the height of the target is less than 1/3 of the height of the trajectory, the depth of the affected space can be determined using the thousandth formula. From the tables we find the angle of incidence 0c = 29 thousandths.
In the case where the target is located on a slope or there is an elevation angle of the target, the depth of the affected space is determined using the above methods, and the result obtained must be multiplied by the ratio of the angle of incidence to the angle of encounter.
The magnitude of the meeting angle depends on the direction of the slope: on the opposite slope, the meeting angle is equal to the sum of the angles of incidence and slope, on the reverse slope - the difference between these angles. In this case, the magnitude of the meeting angle also depends on the angle
Rice. 18. Covered, dead and target space
target elevation: with a negative target elevation angle, the meeting angle increases by the amount of the target elevation angle, with a positive target elevation angle, it decreases by its value.
Note. When falling to the ground or hitting an obstacle at a small angle of contact, the bullet (grenade) ricochets, i.e., it is reflected from the surface of the earth or obstacle and continues to fly along a new trajectory. A ricocheting bullet retains sufficient lethality (penetrating ability) and can inflict defeat.
Example. Determine the depth of the affected space according to the conditions of the previous example, if the target moves along an oncoming slope with a steepness of 3° (50 thousandths).
Solution. Finding the meeting angle. It is equal to 79 thousandths (29+50); the depth of the affected space on the slope (Ppm) will be equal to
The target space to some extent compensates for errors made when choosing a sight, and allows you to round up the measured distance to the target.
To increase the depth of the affected area on sloping terrain, the firing position must be chosen so that the terrain at the enemy’s location, if possible, coincides with the extension of the aiming line.
46. The space behind cover that is not penetrated by a bullet, from its crest to the meeting point is called covered space
(Fig. 18). The greater the height of the shelter and the flatter the trajectory, the greater the covered space.
The part of the covered space in which the target cannot be hit with a given trajectory is called dead (unhittable) space
. The greater the height of the cover, the lower the height of the target and the flatter the trajectory, the greater the dead space. The other part of the covered space in which the target can be hit is the target space.
The depth of the covered space (Dp) can be determined from tables of the excess of trajectories above the line of sight. By selection, an excess is found that corresponds to the height of the shelter and the distance to it. After finding the excess, the corresponding sight setting and firing range are determined. The difference between a certain firing range and the distance to cover represents the depth of the covered space.
The depth of dead space (MD) is equal to the difference between the covered and the affected space.
Example. Determine the depth of the covered, target and dead space when firing from a Kalashnikov light machine gun at running enemy infantry (target height 1.5 m) behind a cover 3 m high. The distance to the cover is 300 m.
Solution.
1. According to the table of excess of average trajectories over the aiming line, we find by selection that at a distance of 300 m the excess of 3 m corresponds to a trajectory with sight 7 (firing range 700 m).
2. Determine the depth of the covered space:
Pp = 700-300 = 400 m.
3. Using the table of excess of average trajectories, we determine the depth of the target space when firing with a sight of 7; it is equal to 75 m.
4. Determine the depth of dead space:
Mpr-Pp—Ppr=400—75=325 m.
If the height of the shelter does not exceed the narrow height of the trajectory, then the depth of the covered and dead space can be determined using the formulas:
where Pp is the covered space in meters;
Mpr - dead space in meters;
By is the height of the shelter in meters;
Vts — target height in meters;
c—meeting angle in thousandths.
From machine guns on machine guns, the depth of the covered space can be determined by the aiming angles
. To do this, you need to install a sight corresponding to the distance to the cover, and aim the machine gun at the crest of the cover. After this, without disrupting the machine gun's aim, aim under the base of the shelter. The difference between these sights, expressed in meters, is the depth of the covered space. It is assumed that the terrain behind the cover is a continuation of the aiming line directed under the base of the cover.
Knowing the size of covered and dead space allows you to correctly use shelters to protect against enemy fire, as well as take measures to reduce dead spaces by correctly choosing firing positions and firing at targets from weapons with a more forward trajectory.
Trajectories of guided projectiles.
In the case of guided projectiles, the already complex task of describing the trajectory is complicated by the fact that a system of equations called guidance equations is added to the equations of motion of a rigid body, which relates the deviations of the projectile from a given trajectory with corrective actions. The essence of projectile flight control is this. If in one way or another, using the equations of motion, a deviation from a given trajectory is determined, then, based on the guidance equations, a corrective action is calculated for this deviation, for example, turning the air or gas rudder, changing thrust. This corrective action, changing certain terms of the equations of motion, leads to a change in the trajectory and a decrease in its deviation from the given one. This process is repeated until the deviation is reduced to an acceptable level.
EXTERNAL BALLISTICS
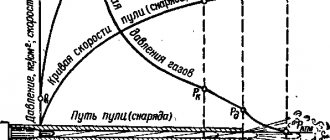
External ballistics deals with the movement of projectiles in the space between the launcher and the target. When a projectile is set in motion, its center of mass traces a curve in space called a trajectory. The main task of external ballistics is to describe this trajectory by determining the position of the center of mass and the spatial position of the projectile as a function of flight time (time after launch). To do this, you need to solve a system of equations that takes into account the forces and moments of force acting on the projectile.
Gas gun.
The gas gun consists of three main parts, shown in Fig. 3: compression section, restriction section and launch barrel. A conventional powder charge is ignited in the chamber, which causes the piston to move down the barrel compression section and compress the helium gas filling the bore. When the helium pressure increases to a certain level, the diaphragm ruptures. A sudden burst of high-pressure gas pushes the projectile out of the launch barrel, and the restrictive section stops the piston. The speed of a projectile fired by a gas gun can reach 5 km/s, while for a conventional gun this is a maximum of 2000 m/s. The higher efficiency of the gas gun is explained by the low molecular weight of the working substance (helium) and, accordingly, the high speed of sound in helium acting on the bottom of the projectile.
Reactive systems.
Barrel projectile acceleration systems no longer meet the ever-increasing demands of the military in terms of range, rate of fire, shooting accuracy and versatility. Through the efforts of science and technology, rocket and air-breathing engines have achieved such perfection that modern types of ballistic weapons are built almost exclusively on jet propulsion. Liquid (LPRE) and solid (solid propellant) rocket engines are widely used. See also ROCKET.; ROCKET WEAPONS.
Rocket launchers perform essentially the same functions as artillery guns. This installation plays the role of a fixed support and usually sets the initial direction of flight of the missile. When launching a guided missile, which, as a rule, has an on-board guidance system, the precise aiming required when firing a gun is not required. In the case of unguided missiles, the launcher guides must place the missile on a trajectory leading to the target.
Trajectories of a material point.
Another special case is the movement of a material point; here the projectile is considered as a material point, and its drag (the force of air resistance acting in the opposite direction tangential to the trajectory and slowing down the movement of the projectile), gravity, the speed of rotation of the Earth and the curvature of the earth's surface are taken into account. (The rotation of the Earth and the curvature of the earth's surface can be ignored if the flight time along the trajectory is not very long.) A few words should be said about drag. The force of drag D exerted on the movement of the projectile is given by the expression
D = rSv2CD(M),
where r is the air density, S is the cross-sectional area of the projectile, v is the speed of movement, and CD (M) is a dimensionless function of the Mach number (equal to the ratio of the projectile speed to the speed of sound in the medium in which the projectile moves), called the drag coefficient. Generally speaking, the drag coefficient of a projectile can be determined experimentally in a wind tunnel or on a test site equipped with precision measuring equipment. The task is made easier by the fact that for projectiles of different diameters the drag coefficient is the same if they have the same shape.
The theory of the motion of a material point (although it does not take into account many forces acting on a real projectile) describes with a very good approximation the trajectory of missiles after the engine stops operating (in the passive part of the trajectory), as well as the trajectory of conventional artillery shells. Therefore, it is widely used to calculate data used in the targeting systems of weapons of this kind.
Application.
The use of ballistics in combat involves the location of the weapon system in a location that would allow it to quickly and effectively hit the intended target with minimal risk to operating personnel. Delivery of a missile or projectile to a target is usually divided into two stages. At the first, tactical, stage, the combat position of barrel weapons and ground-based missiles or the position of the carrier of air-launched missiles is selected. The target must be within the warhead delivery radius. At the shooting stage, aiming is carried out and shooting is carried out. To do this, it is necessary to determine the exact coordinates of the target relative to the weapon - azimuth, elevation and range, and in the case of a moving target - its future coordinates, taking into account the time of flight of the projectile.
Before firing, adjustments must be made for changes in muzzle velocity due to bore wear, powder temperature, variations in projectile weight and ballistic coefficients, as well as adjustments for constantly changing weather conditions and associated changes in atmospheric density, wind speed and direction. In addition, corrections must be made for projectile derivation and (at long ranges) for the rotation of the Earth.
With the increasing complexity and expansion of the range of problems of modern ballistics, new technical means have appeared, without which the possibilities for solving current and future ballistic problems would be greatly limited.
Calculations of near-Earth and interplanetary orbits and trajectories, taking into account the simultaneous movement of the Earth, the target planet and the spacecraft, as well as the influence of various celestial bodies, would be extremely difficult without computers. The approach speeds of hyper-speed targets and projectiles are so high that solving shooting problems on the basis of conventional tables and manually setting shooting parameters is completely excluded. Currently, firing data from most weapon systems is stored in electronic data banks and quickly processed by computers. The computer's output commands automatically position the weapon at the azimuth and elevation required to deliver the warhead to the target.